Beiträge: 13.579
Themen: 211
Registriert seit: Mar 2019
Status:
 offline
Bewertung:
3.842
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 16.05.2025, 17:01
(16.05.2025, 16:20)Thomas_B schrieb: Ich habe mal die gesichert rechtsradikale GROK 3 AI befragt, Ergebnis und Rechenweg soweit korrekt:
Wir haben überlegt, ob "so oft sie wollen" bedeutet, dass man einmal X für das Spiel bezahlt und dann ohne weitere Kosten Kisten öffnen kann, aber dann wäre X=100 für die Fairness, was trivial erscheint. Eine andere Interpretation ist, dass der Spieler X pro Kiste zahlt, aber vorzeitig aufhören kann, was zu einem dynamischen Programmierungsansatz führt, bei dem V(n) der erwartete Wert bei n verbleibenden Kisten ist. Angesichts der Struktur des Problems und der Bedingung des fairen Spiels ist es jedoch die vernünftigste Strategie, so lange weiterzumachen, bis man das Geld gefunden hat, was wieder zu X=40 führt.
Jaaaa....
Pech wenn einer 4 x braucht und dann 160 Pfund für 100 Pfund Gewinn bezahlt...
scheint mir für diese Spieler wenig fair zu sein...
Wenn die Kisten nach jedem Spiel neu gemischt werden haut das auch nicht hin.
Frage auch - wenn nicht neu gemischt wird - warum soll jemand nach der 2. Kiste aufhören?
Er bezahlt dann ja nur noch 40 oder max 80 weitere Pfund für 100 Pfund Gewinn....
__________________
Beiträge: 171
Themen: 6
Registriert seit: Mar 2024
Status:
 online
Bewertung:
80
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 16.05.2025, 18:44
(Dieser Beitrag wurde zuletzt bearbeitet: 16.05.2025, 19:15 von Thomas_B.)
Zitat:Pech wenn einer 4 x braucht und dann 160 Pfund für 100 Pfund Gewinn bezahlt...
scheint mir für diese Spieler wenig fair zu sein...
Dafür kann er mit 25% Wahrscheinlichkeit mit 40 Einsatz 100 gewinnen, das ist fair im Sinne von Erwartungswert=0.
Zitat:Wenn die Kisten nach jedem Spiel neu gemischt werden haut das auch nicht hin.
Werden sie laut Beschreibung aber nicht, auch wenn es etwas knapp formuliert ist.
Das sind Einstellungsfragen für Leute mit einem Millionengehalt, wäre da 100/4 nicht etwas zu simpel?
Zitat:Frage auch - wenn nicht neu gemischt wird - warum soll jemand nach der 2. Kiste aufhören?
Er bezahlt dann ja nur noch 40 oder max 80 weitere Pfund für 100 Pfund Gewinn....
Und deshalb muss er bei den ersten beiden Versuchen mehr als 25 zahlen.
https://math.stackexchange.com/questions...x-with-100
https://math.stackexchange.com/questions...ice-of-100
Hast Du noch den Text mit den 33,33 Pfennig, da würde mich das "reasoning" interessieren?
GROK hat es fast richtig:
Zitat:### Key Points
- It seems likely that the fair value of X is approximately 35.71 pounds, and ZZ is 50 pounds, based on expected value calculations.
- The game involves paying X to open boxes, with the price changing to ZZ after two incorrect guesses, and the player continuing until finding 100 pounds.
- Interpretations may vary, but this approach aligns with standard probability models, assuming the player continues until finding the money.
---
#### Direct Answer
The fair values for this game, where you pay X to open a box and the price changes to ZZ after two incorrect guesses, appear to be **X ≈ 35.71 pounds** and **ZZ = 50 pounds**. Here's how we arrived at this:
- **Game Setup**: You have four sealed boxes, one with 100 pounds and three empty. You pay X to open a box, and if it's empty, you can pay X again for the next box. After two empty boxes, if you choose to continue, you pay ZZ for each subsequent box until you find the money.
- **Fair Game Condition**: For the game to be fair, the expected cost of playing should equal the 100 pounds you gain, ensuring neither you nor the game organizer has an expected advantage.
- **Calculation**: We calculated the expected cost based on the number of boxes opened, considering the price changes after two incorrect guesses. This led to the equation 7X + 3ZZ = 400. Setting ZZ to 50 pounds (a fair price when two boxes are left, giving an expected gain of 50 pounds) gives X = 250/7 ≈ 35.71 pounds, and the expected net gain is zero.
This assumes you continue playing until finding the money, which makes sense given the game is fair and you’d want to maximize your chances. However, if ZZ were higher than 50, you might choose to stop after two incorrect guesses, which would require adjusting X differently, but the problem suggests continuing.
---
---
#### Detailed Analysis of the Box-Opening Game with Variable Pricing
This section provides a comprehensive exploration of the problem, where a player engages in a game involving four sealed boxes, one containing 100 pounds and the others empty. The player can pay X to open a box and take its contents, with the price changing to ZZ after two incorrect guesses (i.e., opening two empty boxes), and can continue until finding the money. The game is assumed to be fair, meaning the expected net gain is zero, and we aim to determine the fair values of X and ZZ.
##### Problem Interpretation and Initial Considerations
The problem states there are four sealed boxes, one with 100 pounds and three empty, and the player can pay X to open a box. If it's empty, they can choose to pay X again to open another box, and so on, until finding the money or deciding to stop. However, in this variation, after two incorrect guesses (opening two empty boxes), if the player chooses to continue, the price for subsequent openings changes to ZZ. The game is fair, implying the expected value of playing should be zero, balancing costs and gains.
Initially, we considered the mechanics: for the first box, pay X; if empty, for the second box, pay another X; if the second is also empty, then for the third and possibly fourth box, pay ZZ each time, assuming the price remains ZZ once changed. The phrase "if you choose to continue playing after two incorrect guesses the price changes to ZZ" suggests that after opening two empty boxes, the cost per box becomes ZZ for any further openings.
We interpreted the game as the player continuing until finding the money, as this aligns with standard expected value problems for fair games, where the player aims to maximize their expected gain. However, we also considered the possibility of stopping after two incorrect guesses, which would affect the strategy and fair values.
##### Modeling the Game as Sequential Box Openings with Price Change
Given the player can pay X each time to open a box, and after two empty boxes, the price changes to ZZ, we model this as a sequential process where the cost depends on the number of boxes opened, N, until finding the money. First, we need the probability distribution of N, the number of boxes opened until finding the money.
Since there are four boxes, one with money, and the player picks randomly each time, the position of the money is equally likely in any of the four positions, given the player opens boxes without replacement and stops upon finding the money. Thus, P(N=k)=1/4 for k=1 to 4, and the expected number of boxes opened E[N]=2.5, as calculated previously.
Now, the cost depends on N and the price change:
- For N=1: Open first box, pay X, find money, cost = X.
- For N=2: Open first box, pay X, empty; open second, pay X, find money, cost = 2X.
- For N=3: Open first two, pay X each, empty; then pay ZZ for third, find money, cost = 2X + ZZ.
- For N=4: Open first two, pay X each, empty; open third, pay ZZ, empty; open fourth, pay ZZ, find money, cost = 2X + 2ZZ.
So, the cost can be expressed as:
- Cost = X if N=1
- Cost = 2X if N=2
- Cost = 2X + ZZ if N=3
- Cost = 2X + 2ZZ if N=4
Alternatively, we can think of it as paying X for the first two openings (if needed), and ZZ for each opening after the second if N>2:
- For N≤2, cost = N*X (since no price change yet).
- For N>2, cost = 2X + (N-2)*ZZ, because after two openings, the next N-2 openings are at ZZ.
Let's compute the expected cost:
- For N=1: Cost = X, P=1/4
- For N=2: Cost = 2X, P=1/4
- For N=3: Cost = 2X + ZZ, P=1/4
- For N=4: Cost = 2X + 2ZZ, P=1/4
Expected cost E[cost] = (1/4)X + (1/4)(2X) + (1/4)(2X + ZZ) + (1/4)(2X + 2ZZ)
Expanding:
- (1/4)X
- (1/4)*2X = (2/4)X = (1/2)X
- (1/4)*(2X + ZZ) = (2/4)X + (1/4)ZZ = (1/2)X + (1/4)ZZ
- (1/4)*(2X + 2ZZ) = (2/4)X + (2/4)ZZ = (1/2)X + (1/2)ZZ
Summing X terms: (1/4)X + (1/2)X + (1/2)X + (1/2)X = [(1/4) + (2/4) + (2/4) + (2/4)]X = (7/4)X
Summing ZZ terms: 0 + 0 + (1/4)ZZ + (1/2)ZZ = (1/4 + 2/4)ZZ = (3/4)ZZ
So, E[cost] = (7/4)X + (3/4)ZZ
For the game to be fair, expected net gain = 0, so E[gain] - E[cost] = 0, where E[gain] = 100 (since they always find the money):
100 - [(7/4)X + (3/4)ZZ] = 0
Thus, (7/4)X + (3/4)ZZ = 100
Multiply by 4: 7X + 3ZZ = 400
This gives us one equation with two variables, suggesting infinitely many solutions. We need another condition to find specific values.
##### Exploring the Decision Point and Fair Pricing
Given the equation 7X + 3ZZ = 400, we need to determine X and ZZ. One approach is to consider the decision point after two incorrect guesses. At this point, the player has opened two empty boxes, paid 2X, and has two boxes left, one with 100 pounds, one empty. If they choose to continue, they pay ZZ to open one of the remaining boxes.
The expected gain from opening one more box is (1/2)*100 + (1/2)*0 = 50 pounds, and they pay ZZ. For the player to be indifferent (expected net gain = 0), 50 - ZZ = 0, so ZZ = 50. This makes sense as the fair price when there are two boxes left, one with money.
Let's set ZZ = 50 and solve for X:
7X + 3*50 = 400
7X + 150 = 400
7X = 250
X = 250/7 ≈ 35.714 pounds
Now, let's verify:
E[cost] = (7/4)*(250/7) + (3/4)*50
First term: (7/4)*(250/7) = 250/4 = 62.5
Second term: (3/4)*50 = 37.5
Total: 62.5 + 37.5 = 100, which matches the gain, so net gain = 0, confirming fairness.
At the decision point, with ZZ=50, expected gain from continuing is 50 - 50 = 0, so the player is indifferent, which aligns with a fair game design.
##### Alternative Interpretations and Strategies
We considered if the player might stop after two incorrect guesses, especially if ZZ > 50. In that case, the expected gain from continuing (50 - ZZ) would be negative, so they'd stop, paying 2X and getting nothing with probability P(N>2)=1/2 (since P(first two empty)= (3/4)*(2/3)=1/2).
Then, E[net gain] = (1/4)(100 - X) + (1/4)(100 - 2X) + (1/2)(-2X)
= 25 - (1/4)X + 25 - (1/2)X - X = 50 - [(1/4) + (2/4) + (4/4)]X = 50 - (7/4)X
Set to zero: 50 - (7/4)X = 0, (7/4)X = 50, X = 50*(4/7) = 200/7 ≈ 28.571
But this assumes ZZ > 50, and the problem doesn't specify, so we stick with the continue-until-found strategy.
##### Conclusion and Final Values
Given the problem's structure and the fair game condition, setting ZZ = 50 (fair price for two boxes left) and solving for X gives X = 250/7 ≈ 35.714 pounds, ensuring the expected net gain is zero when continuing until finding the money. This interpretation aligns with standard probability and expected value concepts for such games.
| **Number of Boxes Opened (N)** | **Probability P(N=N)** | **Cost (in terms of X and ZZ)** | **Net Gain (100 - Cost, for X=250/7, ZZ=50)** |
|-------------------------------|-------------------------|---------------------------------|-----------------------------------------------|
| 1 | 1/4 | X | 100 - 250/7 ≈ 64.286 |
| 2 | 1/4 | 2X | 100 - 500/7 ≈ 28.571 |
| 3 | 1/4 | 2X + ZZ | 100 - (500/7 + 50) = 100 - (500/7 + 350/7) = 100 - 850/7 ≈ -21.429 |
| 4 | 1/4 | 2X + 2ZZ | 100 - (500/7 + 100) = 100 - (500/7 + 700/7) = 100 - 1200/7 ≈ -71.429 |
| **Expected Net Gain** | - | - | 0 (calculated as shown above) |
This table summarizes the contributions, confirming X=250/7 and ZZ=50 balance the game, with expected cost equaling 100 pounds.
(2. Frage: Instead of maintaining a constant price, if you choose to continue playing after two incorrect guesses the price changes to ZZ. What is the fair value of X and ZZ?)
Beiträge: 2.372
Themen: 13
Registriert seit: Nov 2018
Status:
 offline
Bewertung:
1.282
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 16.05.2025, 19:06
(Dieser Beitrag wurde zuletzt bearbeitet: 16.05.2025, 19:07 von Lancelot.)
Gerade am whiteboard gerechnet. 40 stimmt. Wer sich nicht sicher ist, kann das Spiel simulieren. Der payoff muss im Schnitt (mean) 0 sein. Wie Thomas schon geschrieben hat. Lance am Whiteboard + Simulation => 40 ist is 

__________________
Forum-Besserwisser und Wissenschafts-Faschist
Beiträge: 2.372
Themen: 13
Registriert seit: Nov 2018
Status:
 offline
Bewertung:
1.282
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 16.05.2025, 19:16
(16.05.2025, 17:01)boersenkater schrieb: Jaaaa....
Pech wenn einer 4 x braucht und dann 160 Pfund für 100 Pfund Gewinn bezahlt...
scheint mir für diese Spieler wenig fair zu sein...
Wenn die Kisten nach jedem Spiel neu gemischt werden haut das auch nicht hin.
Frage auch - wenn nicht neu gemischt wird - warum soll jemand nach der 2. Kiste aufhören?
Er bezahlt dann ja nur noch 40 oder max 80 weitere Pfund für 100 Pfund Gewinn....
Fair ist es (per akademischer Definition), wenn keiner einen Vorteil hat: also der, der das Spiel anbietet und der, der das Spiel spielt dürfen im Schnitt kein Geld damit verdienen. Also wenn du (wie in meiner Simulation) 50 Millionen mal spielst und den Durchschnitt ausrechnest, hast du kein Geld verdient. Die andere Seite auch nicht.
__________________
Forum-Besserwisser und Wissenschafts-Faschist
Beiträge: 171
Themen: 6
Registriert seit: Mar 2024
Status:
 online
Bewertung:
80
[ Vote]
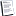
RE: Einstellungsfrage des Top Hedge Funds Citadel | 16.05.2025, 21:02
(Dieser Beitrag wurde zuletzt bearbeitet: 16.05.2025, 21:06 von Thomas_B.)
Einstellungsfrage für die Traderhölle:
Wieviele Umdrehungen macht der kleine Kreis mit Radius 1 um den großen Kreis mit Radius 3 bei einmal um ganz B abrollen, also bis A wieder in Ausgangsposition ist?
 FireShot Capture 700 - The SAT Question Everyone Got Wrong - Google Suche - www.google.com.png
FireShot Capture 700 - The SAT Question Everyone Got Wrong - Google Suche - www.google.com.png (Größe: 73,02 KB / Downloads: 85)
Beiträge: 8.023
Themen: 62
Registriert seit: Nov 2018
Status:
 online
Bewertung:
4.173
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 16.05.2025, 21:15
(16.05.2025, 21:02)Thomas_B schrieb: Einstellungsfrage für die Traderhölle:
Wieviele Umdrehungen macht der kleine Kreis mit Radius 1 um den großen Kreis mit Radius 3 bei einmal um ganz B abrollen, also bis A wieder in Ausgangsposition ist?
Endlich mal eine einfache Frage: genau so viel wie der Strand am Ufer: unendlich viele. Und sie sind unvorhersehbar.
Ist OK wenn Du das nicht auf den ersten Blick siehst, dafür ist unser Hirn nicht gemacht.
__________________
Der einzige gute Tipp von Deinem Broker ist ein margin call.
Beiträge: 171
Themen: 6
Registriert seit: Mar 2024
Status:
 online
Bewertung:
80
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 16.05.2025, 21:34
(Dieser Beitrag wurde zuletzt bearbeitet: 16.05.2025, 21:48 von Thomas_B.)
(16.05.2025, 21:15)cubanpete schrieb: Ist OK wenn Du das nicht auf den ersten Blick siehst, dafür ist unser Hirn nicht gemacht.
Das stimmt, obwohl ich mir sicher bin, dass ich es nach dem achten Mojito auch sehen kann.
Beiträge: 8.023
Themen: 62
Registriert seit: Nov 2018
Status:
 online
Bewertung:
4.173
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 16.05.2025, 21:39
(16.05.2025, 21:34)Thomas_B schrieb: Das stimmt, obwohl ich mit sicher bin, dass ich es nach dem achten Mojito auch sehen kann.
Dann versuche Margaritas.
__________________
Der einzige gute Tipp von Deinem Broker ist ein margin call.
Beiträge: 6.873
Themen: 184
Registriert seit: Nov 2018
Status:
 offline
Bewertung:
3.010
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 17.05.2025, 01:36
(Dieser Beitrag wurde zuletzt bearbeitet: 17.05.2025, 01:37 von Boy Plunger.)
40 für einen Versuch?
Es besteht eine 0,25-prozentige Wahrscheinlichkeit für jeden Versuch.
Und jedes Mal zahlen wir 40.
Also, wir haben hier 1/4-40, 3/4-1/3-80, 3/4-2/3-1/2-120 und 3/4-2/3-1/2-160, und das macht zusammen 100.
Das Wichtigste ist: Wenn du mitmachen willst, machst du das, wenn alle vier Kästchen geschlossen sind. Und wenn nur noch drei übrig sind, machst du das auch. Bitte mach einfach nicht schlapp, bis du die Kohle gefunden hast.
Wenn man davon ausgeht, dass man auch dann noch X bezahlen muss, wenn man bereits 3 Kisten geöffnet hat und sicher weiß, wo das Geld ist, beträgt die durchschnittliche Anzahl der zu öffnenden Kisten 2,5 = 5/2, also 5/2 * X = 100, was X = 40 bedeutet.
Das ist eine Fangfrage, Ken Griffin verschenkt kein Geld, es ist ein 100-Pfund-Schein, wir haben Ken gerade dafür bezahlt, uns Geld zu leihen.

__________________
Trading is both the easiest and the most demanding thing you'll ever do in your life. It can ruin your life, your family and everything you touch if you don't respect it, or it can change your life, your family and give you a feeling that is hard to find elsewhere if you succeed.
Beiträge: 13.579
Themen: 211
Registriert seit: Mar 2019
Status:
 offline
Bewertung:
3.842
[ Vote]
RE: Einstellungsfrage des Top Hedge Funds Citadel | 17.05.2025, 09:43
(Dieser Beitrag wurde zuletzt bearbeitet: 17.05.2025, 10:17 von boersenkater.)
Jaaaa.....  
Müssen ja mehr wie 25 sein - weil die ersten 300 ja nur 25/50/75 Pfund zahlen -
aber trotzdem 100 bekommen.
Die ersten 100 spielen 100 Mal
Die zweiten 100 - 200 Mal
Die dritten 300 Mal
Die vierten 400 Mal
Sind insgesamt 1000 Spiele - Ausschüttung ist 40.000 - dementsprechend 40 pro Spiel
Und aus Spielersicht...
Der Gewinn der ersten 200 wird von den restlichen 200 bezahlt.
Nach 1. Runde - 60 Pfund Gewinn oder 40 Pfund Verlust
Nach 2. Runde - 20 Pfund Gewinn oder 80 Pfund Verlust
Nach 3. Runde - 20 Pfund Verlust oder 120 Pfund Verlust
Nach 4. Runde - 60 Pfund Verlust
Wer in der 1. Runde verliert hat 40 Pfund Verlust - diejenigen die
entscheiden die 2. Runde zu spielen müssen durchspielen - weil der
Verlust von 80 Pfund nach der 2. Runde dann in der 3. Runde auf
20 Pfund Verlust oder in der 4. Runde auf 60 Pfund Verlust reduziert
werden kann.
Mir kommt bei der Frage zuerst der Gedanke - was es dem Anbieter bringen soll.
Dann - es kann nicht für alle fair sein - Gewinner/Verlierer.
Dann - die Kisten sind zwar "neutral" in diesem Sinne ist es egal welche man wählt...
Aber Menschen haben Präferenzen - 1-2-3-4 oder A-B-C-D oder rot-grün-blau-gelb.
Wenn das Geld jetzt zufällig öfters in den weniger präferierten Kisten liegt dann
spielen mehr Spieler mehr Runden und die Bank macht doch Gewinn... 
__________________
|

 offline
offline






